Un concepto, quizás no tan conocido, pero igualmente importante: el Ángulo Áureo. Es decir, la relación angular de proporción entre dos segmentos circulares:
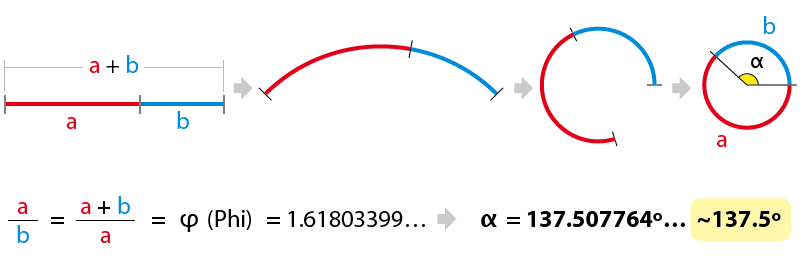
Con estos dos segmentos circulares se sigue cumpliendo la misma proporcionalidad áurea, pero en este caso el valor del ángulo formado por el menor de ellos es otro número irracional, que podemos simplificar y redondear como 137,5º
Y resulta que ese valor está muy presente en la naturaleza.Fijáos en al siguientes figuras:
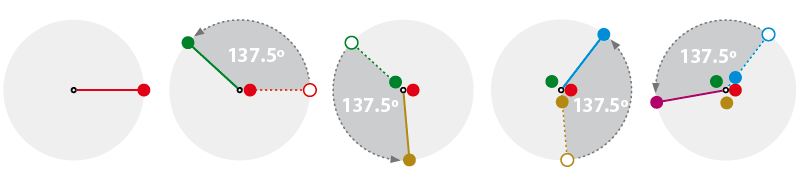
— Aportamos un primer punto de color rojo.
— Giramos 137,5º
— Añadimos un segundo punto de color verde y hacemos que la anterior se vaya hacia el centro.
— Giramos otros 137,5º
— Añadimos un tercer punto de color tostado y hacemos que la anterior se vaya hacia el centro, hasta tocar con la primera.
— Giramos otros 137,5º…
… y así sucesivamente, punto tras punto, iríamos obteniendo paulatinamente unas distribuciones como las que tenéis en las siguientes figuras.

Esta figura representa la forma más compacta en la que pueden agrupar un conjunto sobre un plano.
Además esta figura tiene un parecido grande a la forma que estan agrupadas las semillas de un girasol. Siempre se ha dicho: la naturaleza es sabia.
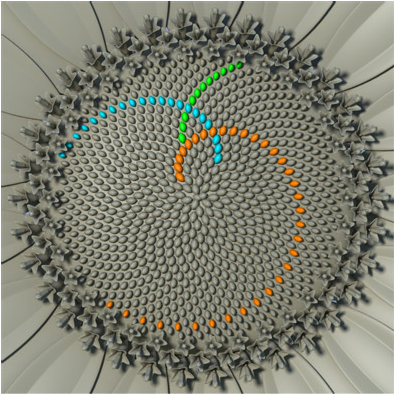
Si observáis atentamente la configuración de las semillas veréis cómo aparecen una serie de patrones en espiral. En la ilustración tenéis resaltadas tres de las tipologías de espirales que podemos encontrar.
Si nos centramos en una de las espirales obtendremos un número que se encuentra en la Sucesión Fibonacci.



El 55, 34 y 21 todas ellas se encuentran en la Sucesión Fibonacci

Y es que cualquier cosa hecha de esta manera, con el ángulo áureo, va a contener un número de la sucesión Fibonacci, ya que la sucesión fibonacci y la proporción áurea (divina proporción) están profundamente relacionados.
Sigues sin entender?

La cabeza de una flor se compone de pequeñas semillas que se producen en el centro, y luego emigran hacia el exterior para llenar eventualmente todo el espacio. Cada semilla nueva aparece en un cierto ángulo en relación a la anterior. Por ejemplo, si el ángulo es de 90 grados, es decir 1 / 4 de vuelta.
Por supuesto, esto no es la forma más eficaz de llenar el espacio. De hecho, si el ángulo entre la aparición de cada semilla es una parte de un giro que corresponde a una fracción simple, 1 / 3, 1 / 4, 3 / 4, 2 / 5, 3 / 7, etc (que es un mero número racional), siempre se obtiene una serie de líneas rectas. Si uno quiere evitar este patrón rectilíneo, es necesario escoger una parte del círculo que es un número irracional (o una fracción no-simple). Si esto último es bien aproximada por una fracción simple, se obtiene una serie de líneas curvas (brazos en espiral), que aún así no llena el espacio a la perfección.
Con el fin de optimizar el llenado, es necesario elegir el número más irracional que hay, es decir, el que menos bien aproximada por una fracción. Este número es exactamente la sección áurea. El ángulo correspondiente, el ángulo de oro, es 137,5 grados. (Se obtiene multiplicando el porcentaje de no enteros de la sección áurea en 360 grados y, puesto que se obtiene un mayor ángulo de 180 grados, al tomar su complemento). Con esta perspectiva, se obtiene el óptimo de llenado, es decir, el mismo espaciado entre todas las semillas.
Este ángulo tiene que ser elegido de manera muy precisa: las variaciones de 1 / 10 de un grado destruyen por completo la optimización. Cuando el ángulo es exactamente la proporción áurea, y sólo éste, dos familias de espirales (uno en cada sentido) son visibles a continuación: sus números se corresponden con el numerador y el denominador de 2 números consecutivos de la sucesión de Fibonacci, que se ha demostrado que convergen hacia el valor de la proporción áurea es de 1.6180339 ... (En la imagen que tenemos 21/34, los términos 7 y 8 de la secuencia de Fibonacci).
Nota: entre mayor sea, más patrones circulares se pueden apreciar

Estos números son precisamente los de la secuencia de Fibonacci (entre más grande es el número, mejor será la aproximación) y la elección de la fracción depende de las vueltas de tiempo entre la aparición de cada una de las semillas en el centro de la flor.
Por ello, el número de espirales en los centros de girasol, y en los centros de flores en general, corresponden a un número de Fibonacci. Por otra parte, en general, los pétalos de las flores se forman en el extremo de un de las familias de espiral (cierto, cuento con 34 para este girasol). Esta es, pues, también por qué el número de pétalos corresponde en promedio a un número de Fibonacci.


