Es una serie muy famosa y reconocida descubierta Leonardo de Pisa, una matemático italiano del siglo XIII, también conocido por su apodo Fibonacci.
Se trata de una sucesión infinita de números naturales donde el primer valor es 0, el siguiente es 1 y, a partir de ahí, cada cantidad se obtiene sumando las dos anteriores.
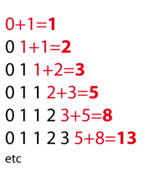
El resultado es una sucesión infinita de números naturales.

Lo curioso es que podemos ver estos números en la naturaleza:
Flores:
| 1 petalo | Cala blanca |  |
| 2 petalos | Euphorbia |  |
| 3 petalos | Trillium |  |
| 5 petalos | Aguileña |  |
| 8 petalos | Sanguinaria |  |
| 13 petalos | Rudbeckia |  |
| 21 petalos | Leucanthemum x superbum (margaritas) |  |
| 34 petalos | Margaritas del campo |  |
| 55, 89 petalos | San Miguel margaritas |  |
| Giraflores |  |
Hay que notar que muchas especies son muy precisos en el número de sus petalos, sin embargo hay otros que tienen el número de sus petalos muy cerca, siendo el promedio el un número fibonacci.
Conejos:Una pareja de conejos tarda un mes en alcanzar la edad fértil, a partir de ese momento cada vez engendra una pareja de conejos, que a su vez, tras ser fértiles engendrarán cada mes una pareja de conejos.
¿Cuántos conejos habrá al cabo de un determinado número de meses?.
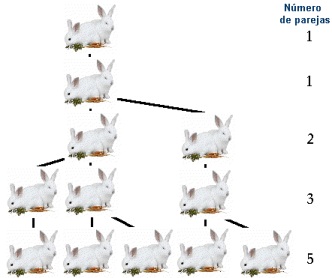
Como podéis ver en el gráfico, el número de parejas a lo largo de los meses coincide con los términos de la sucesión
Abejas:
El número de descendientes en cada generación de una abeja macho o zángano nos conduce a la sucesión de Fibonacci.
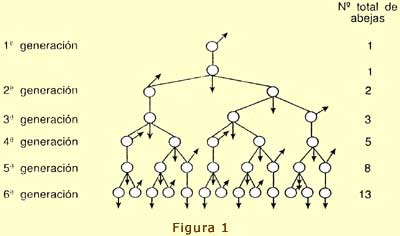
Según se sabe, una vez inseminada la abeja reina por un zángano (de otro enjambre), aquella se queda en su colmena y ya no sale más, dedicándose a la puesta de huevos que ella misma va fecundando o no, dando origen así a abejas obreras, o bien reinas, en el primer caso y machos o zánganos en el segundo. Si observamos el árbol genealógico de un zángano, podemos ver como el número de abejas en cada generación es uno de los términos de la sucesión de Fibonacci.
Ramas y hojas:
Se distribuyen buscando siempre recibir el máximo de luz para cada una de ellas. Por eso ninguna hoja nace justo en la vertical de la anterior. La distribución de las hojas alrededor del tallo de las plantas se produce siguiendo secuencias basadas exclusivamente en estos números.
En la imagen que se ve acontinuación hemos enumerado las hojas y la "x" es el punto de inicio. Se va a contar cuantas hojas toma para que una hoja que casi debajo de la hoja con la "x"

El 3, 5, 8 y 13 son las hojas que estan debajo o cerca de la x, y estos cuarto n&uactue;meros son de Fibonacci. Toma 3 hojas para dar una vuelta, 5 hojas para dar 2 vueltas, etc.
Se estima que el 90% de las plantas exciben este tipo de comportamiento.
Vegetales:
Arriba tenemos la imagen de un coliflor normal, si nos fijamos podemos ver que tiene un patron de espiral (marcadas con rojo y las de sentido contrario en azul), si las contamos podremos notar que hay 5 rojas y 8 azules.


En esta foto tenemos a un romanesco, se ve y sabe como un cruce de brocoli y coliflor; y al igual que el anterior hay un patron de espiral
Cuantos espirales se pueden contar?
21 y 13 respectivamente
2 manos cada uno de ellos tiene...
5 dedos, cada uno con...
3 partes separadas por...
2 nudillos
Pero...siempre van a aparecer números Fibonacci?

El fuchsia siempre tiene 4 petalos.

Existen pimentones con 4 secciones.
Flores con seis petalos
 |  |
| Amaryllis | Narcissus |
Otros ejemplos:
 |  |  |
| Con 4 espirales y 7 espirales en sentido contrario | Con 29 costillas | Con 11 espirales y 17 espirales en sentido contrario |
Asi que queda claro que no todo tienen los números de Fibonacci.
Otra suceción no tan famosa como la de Fibonacci (pero sigue siendo famosa) son los Números Lucas que lo que comienza con 2 y 1, y después, como los números de Fibonacci, que la regla de que la próxima es la suma de las dos anteriores para dar:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 ..
¿Te diste cuenta que el 4, 7, 11, 18 e incluso 29 casos ocurrieron en las fotos no Fibonacci arriba?


