Si tomamos los números de la sucesión fibonacci...

Y hacemos un cuadriculado con estos números, con cada cuadrito con el valor de 1 obtendríamos algo así
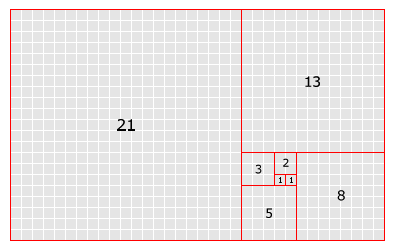
Obtenemos el rectangulo dorado. Ahora este peculiar rectangulo se puede encontrar en muchas partes de la naturaleza, así como en las artes y arquitecturas

Puedes ver el rectangulo dorado en la imagen de arriba?
No? Que tal si te ayudamos un poco.
Primero trasaremos una linea por el techo arruinado

Luego le ponemos el rectangulo dorado
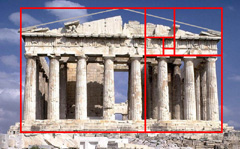
Y encaja perfectamente
En esta pintura incompleta de Leonardo Da Vinci también se puede apreciar


A continuación podemos trazar un cuarto de arco de circunferencia (90º) dentro de cada cuadradito y fácilmente vemos cómo surge la Espiral de Fibonacci
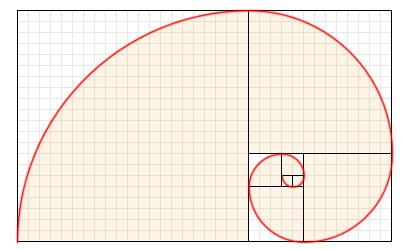
Obtenemos la espiral Fibonacci, una espiral logaritmica con un ratio de 1.618...
Y podemos ver estas espirales en la naturaleza como en creaciones humanas


Y creaciones humanas



Pero no todo es color de rosa, ya que aunque la espiral se parezca mucho a la concha del nautilus

No son iguales, aunque ambos sean espirales logaritmicas tienen un ratio diferente; siendo la del nautilus de 1.24 a 1.43, con un ratio promedio de 1.33, no se acerca al de la espiral Fibonacci que es 1.618...

Pero el rectangulo no es lo único que existe.
El triángulo de oro es un isósceles especiales triángulo. El ángulo superior es de 36 ° mientras que la parte inferior dos ángulos de 72 ° cada uno. A continuación, atraviesan uno de estos ángulos de la base. El triángulo azul resultante:
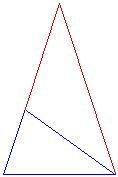
también es un triángulo de oro! Por lo tanto, podemos mantener la bisectriz del ángulo de base para obtener un conjunto de triángulos girando:
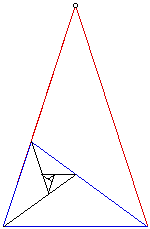
De esto, podemos dibujar una espiral logarítmica similar a la espiral de Fibonacci:
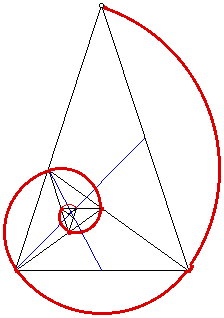
Y este triangulo tambien se puede encontrar en varias partes


Y un poco más complicado en la Mona Lisa



